题目描述
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
代码
public class Solution {
public boolean VerifySquenceOfBST(int [] sequence) {
if(sequence == null || sequence.length == 0) return false;
return func(sequence, 0, sequence.length - 1);
}
private boolean func(int[] array, int l, int r){
if(l == r){
return true;
}
int i = l;
while(array[i] < array[r]){
i++;
}
int k = i;
while(array[k] > array[r]){
k++;
}
boolean left = true;
boolean right = true;
if(i > l){
left = func(array, l, i - 1);
}
if(k > i){
right = ((k == r) && func(array, i, r - 1));
}
//防止第一个array[l]过大, 原地踏步. 不加也可以跑过牛客网的用例
if(i == k && i != r){
return false;
}
return left && right;
}
}
思路
数组: 4 8 6 12 16 14 10
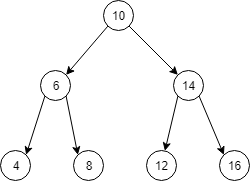
题目中给的二叉树的后续遍历序列, 我们进行还原, 根据还原出来的树, 进行思考.
整棵树为二叉搜索树, 所以它的子树也全为二叉搜索树, 很容易想到利用递归.
每次遍历, 分割数组, 单位数组中的最后一个树, 显然为此次遍历中树的根.
根据数组中根的值, 来进行继续分割数组.
这里会出现临界值, array[left] == array[right]时候, 说明该次遍历是一个叶子节点, 返回true;
如果找到的分割左右子树的下标不符合二叉搜索树, 返回false;
比如k > i but k != r, 说明右子树中存在不大于根节点的数字.
if(i == k && i != r){
return false;
}
如果不加入, 用例数组 100 8 6 12 16 14 10
第一个数字过大, 判断也返回true, 这段代码, 防止这样的原地踏步.
PREVIOUSObject源码分析
NEXTJava 类加载