通常我们需要在队列中选取优先级重要的任务进行处理, 或者在有限的空间去淘汰掉一些元素, 再比如, 在定时任务中, 我们使用线程去检查是否触发任务, 一个一个把任务扫面完, 这样效率太低了, 也可以用堆, 只用去判断最近的一个任务是否可以触发.
了解堆排序之前, 我们需要先了解一下堆这种数据结构.
堆其实可以理解是二叉树的一种, 堆的性质如下:
- 任意节点小于等于(或大于等于)它的所有子节点.
- 堆是一棵完全二叉树.
什么是完全二叉树? 对于深度为K的二叉树.
- 所有叶子节点都出现在K层或者K-1层
- 对于任意节点, “其左子树的节点总是多于右子树的节点” (如果右子树的最大层次为L, 那么左子树的最大层次为L或者L+1
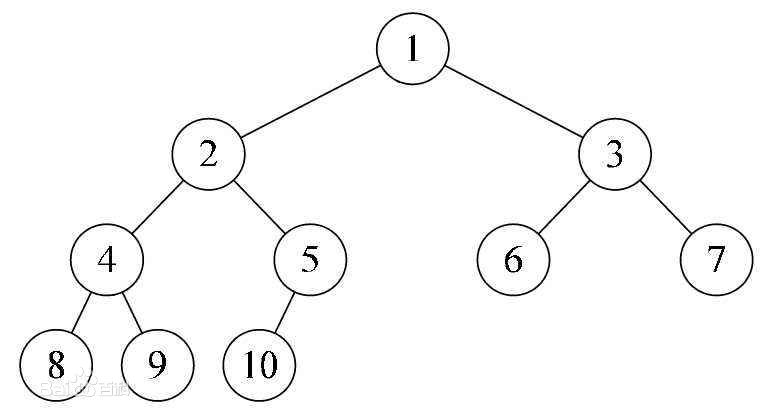
根据堆父节点与子节点的关系.可以将堆分为最大堆与最小堆.
根据完全二叉树的特性. 上面这棵完全二叉树的我们将从左到右转化为一个数组.
[1, 2, ,3 ,4 ,5 ,6, 7, 8, 9 , 10]
最后一个带有节点的树的位置是 array.length / 2 - 1
对于一个有子树的节点i, 它的左子树为2 * i + 1, 右子树为2 * i + 2
了解了这些必要的信息, 堆排序也就不难了.
堆排序是一种改进的选择排序, 我们每次通过构建最大堆或者最小堆, 将父节点与最后一个元素进行交换, 然后依次类推, 排完所有节点就OK了.
构建最大堆或者最小堆.
就是从最后一棵带有子节点的树, 将这颗树进行”最大堆化”, 然后依次递归进行.
直接上代码把, 代码还是比较容易理解的.
这是递归的版本
package com.sortAndSearch;
//堆排序是一种"改进的"选择排序
public class HeapSort implements IArraySort {
@Override
public int[] sort(int[] nums) {
int len = nums.length;
//构成全体最大堆
buildMaxHeap(nums, len);
for (int i = len - 1; i > 0; i--) {
swap(nums, 0, i);
len--;
toMaxHeap(nums, i, len);
}
return nums;
}
private void buildMaxHeap(int[] nums, int len) {
//将整个数组构成最大堆
for (int i = len / 2; i >= 0; i--) {
toMaxHeap(nums, i, len);
}
}
private void toMaxHeap(int[] nums, int i, int len) {
int left = 2 * i + 1;
int right = 2 * i + 2;
int largest = i;
//将由一个父节点和两个子节点(如果存在)的数进行排序.
if (left < len && nums[left] > nums[largest]) {
largest = left;
}
if (right < len && nums[right] > nums[largest]) {
largest = right;
}
if (largest != i) {
swap(nums, i, largest);
//这里i != largest, 以largest为下标的元素已经不是原来那三个数,
// 所以这里不是冗余的操作, 而是交换之后, 原来以nums[largest]为父节点的子树(最大堆)可能会遭到破坏
// 这里重新组建最大堆
toMaxHeap(nums, largest, len);
}
}
private void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
其实递归版本进行了不必要的交换, 我们只需记录要”堆化”的根节点的值, 到最后再”交换”就行了.
非递归版本.
//构建最大堆
private void adjustHeap(int[] nums, int i, int len){
//记录根节点
int temp = nums[i];
//k = k * 1, 往下递归, 以防子树的子节点中仍存在大于根节点的值
for (int k = 2 * i + 1; k < len; k = k * 2 + 1){
//从左右子树中找出最大值.
if (k + 1 < len && nums[k] < nums[k + 1]){
k = k + 1;
}
//如果子树中存在值大于根节点, 那么将根节点赋予最大值
//这里更换i的值, 以便于往下进行迭代
if (nums[k] > temp){
nums[i] = nums[k];
i = k;
}else {
//如果根节点大于左右子树, 那么结束
break;
}
}
nums[i] = temp;
}
public int[] sort2(int[] nums){
int len = nums.length;
for (int i = len / 2 - 1; i >= 0; i--){
adjustHeap(nums, i, len);
}
for (int i = len - 1; i > 0; i--){
swap(nums, i, 0);
adjustHeap(nums, 0, i);
}
return nums;
}
这里也给出构建最小堆的代码
private void toMinHeap(int[] nums, int i, int len){
int temp = nums[i];
for (int k = 2 * i + 1; k < len; k = k * 2 + 1){
if (k + 1 < len && nums[k] > nums[k + 1]){
k = k + 1;
}
if (nums[k] < temp){
nums[i] = nums[k];
i = k;
}else {
break;
}
}
nums[i] = temp;
}
运行结果

PREVIOUSRedis实现分布式锁
NEXT初见Jmeter测试